What is a Residual?

Imagine you're predicting the final score of a basketball game. You estimate the score to be 100-95, but the actual score ends up being 102-95. The difference between what you predicted (100) and the actual outcome (102) is, in a sense, a residual.

More formally in statistics, a residual is the difference between the actual observed value (what really happened) and the predicted value (what your model said would happen). When we use data to make predictions, there's often a gap between our prediction and the actual outcome. This 'gap' is what we call the residual.

To put it into a formula:

     Residual = Observed value – Predicted value 

Why are Residuals Important?

Although residuals might appear as simple errors in prediction, they're a goldmine of information. Here's why they're important:

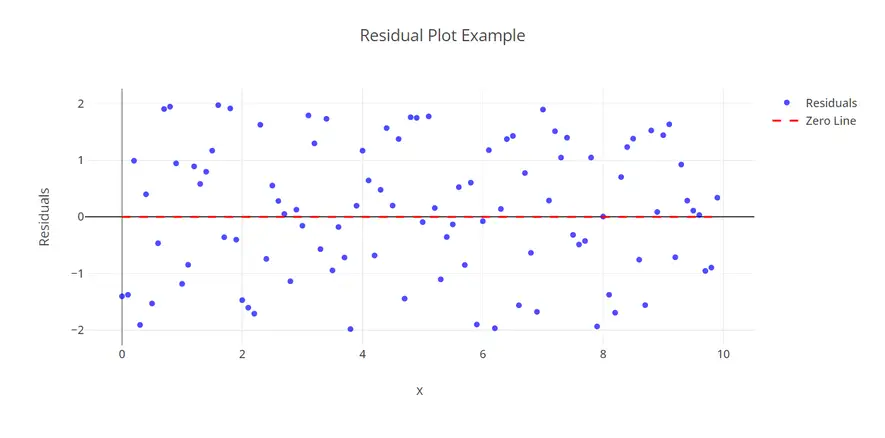
1. Evaluating Model Accuracy: If your model is accurate, your residuals will be scattered randomly and close to zero, with no discernable pattern. If a pattern emerges in your residuals, it's a red flag that your model may not be the best fit for your data.

2. Spotting Outliers: Occasionally, a residual might be significantly larger or smaller than the rest. This can indicate that the corresponding data point is an 'outlier' or an atypical observation, warranting further investigation.

3. Checking Model Assumptions: Many predictive models assume that residuals are normally distributed and exhibit constant variability. By examining the residuals, we can verify whether our data fulfills these assumptions.

Residuals in Linear Regression

Linear regression is a common statistical tool used to predict a dependent variable (like the final score in a basketball game) using one or more independent variables (like team statistics). In the context of linear regression, we calculate the residual for each data point using this formula:

    e = Y - (a + bX)

Here, Y represents the actual observed value, X is the input variable, a and b are coefficients that the model calculates, and (a + bX) is the predicted value. 

Residuals in linear regression inform us about the distance of data points from the regression line (the best fit line through the data). A positive residual means the actual value was higher than the predicted (the model underestimated), and a negative residual means the actual value was lower (the model overestimated).

How to Analyze Residuals?

There are various ways to interpret these residuals:

1. Residual Plots: In a residual plot, residuals (on the vertical axis) are plotted against the input variable (on the horizontal axis). If the points are randomly scattered around the horizontal axis, it implies a well-fitted model. Otherwise, a non-linear model might be more suitable.

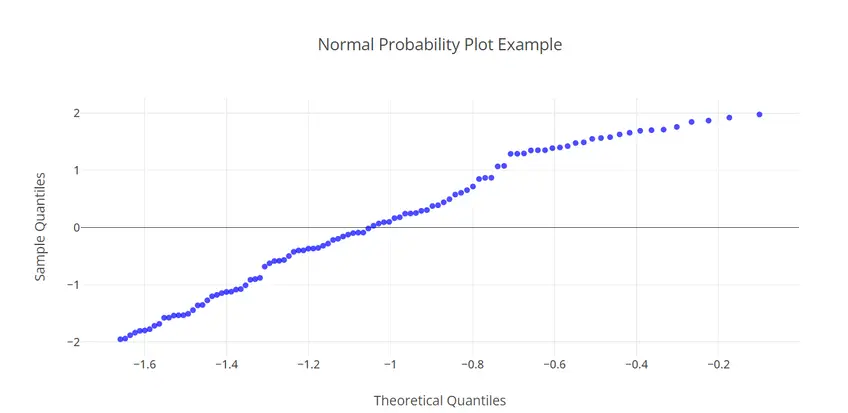
2. Normal Probability Plots: In these plots, residuals are sorted and plotted against their expected values if they were normally distributed. If the points follow a straight line, it indicates our residuals are normally distributed.

In essence, residuals act as a diagnostic tool for our statistical model. They help gauge model performance, signal unusual data points (outliers), and validate if our data meets the model's assumptions. Learning to interpret residuals can significantly boost our predictive models' performance, making our data analysis more robust. However, they're just one part of a broader toolkit for model diagnostics, and for comprehensive analysis, they should be used alongside other methods.

Hey! We just launched a mobile app to make using Z-tables easier! Get it from IOS App Store! Get it from Play Store Get our Z-Table Mobile App!

Step 2: Predict Sales with a Regression Model

To predict sales, we first need a model. In this case, we are going to use a simple linear regression model. The regression model has the form `y = ax + b` where 'x' is our independent variable, 'a' is the slope, and 'b' is the y-intercept.

By using statistical methods (which can be done with software like Python, R, Excel, etc.), we find that the best fit line through our data is represented by the formula: `Sales = 0.7553*Hours + 29.63`. This means that for each additional hour we're open, we predict an increase of approximately 0.7553 in sales, with a baseline (when Hours = 0) sales of 29.63.

With this model, we can calculate the predicted sales for each day:

Let's visualize our observed and predicted sales with a scatter plot:

Step 3: Calculate Residuals

Now that we have our predicted sales, we can calculate the residuals.Residuals represent the difference between the observed and predicted sales. They show us how well our model is predicting sales:

Step 4: Visualize and Interpret the Residuals

Visualizing our residuals can provide useful insights. Residuals represent the error between our model's predictions and the actual sales. If our model is good, residuals should be randomly scattered around zero:

Step 5: Improving Our Predictions

Residuals provide valuable insights for improving our model. By analyzing the distribution and patterns in residuals, we can tweak our model to better fit the data. For example, if residuals show a pattern (such as increasing with X), we may consider a more complex model like polynomial regression.

Looking at our plot, we see that this is the case. The residuals do not show any clear pattern - they're scattered around zero. This suggests that our linear regression model is a good fit for the data. This information is very valuable for our business. It allows us to confidently predict our sales based on how many hours we are open, which in turn enables us to better plan our resources.